Tabeller            
Du använder en tabell för att sammanställa fakta och för att få en bra överblick över den statiskt man har. Ett exempel på detta kan vara att du har skrivit ner temperaturen under en vecka och sammanställt fakta i en tabell.
Frekvenstabeller
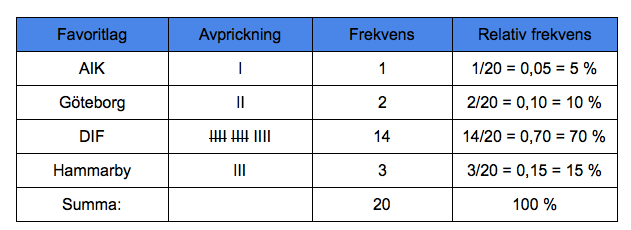
​Frekvens betyder antal och är bra att använda vid undersökningar. Så här kan en frekvenstabell se ut.
I kolumnen (spalten) avprickning  sätter du ett streck för varje svar du får.

​I kolumnen (spalten) frekvens skriver du antalet markerade streck.

​Relativ betyder att jämföra med eller ställa i relation till. DIF är favoritlaget hos 14 av 20 tillfrågade personer. Det är
​70 % av de tillfrågade. Man berättar alltid om relativ frekvens i procentform.
Diagram
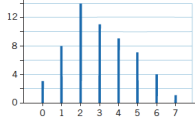
Ett diagram är en bild över fakta ur en tabell. Du kan välja ett passande diagram beroende på vad du vill visa. Fyra vanliga diagram är stapeldiagram, stolpdiagram, linjediagram och cirkeldiagram. 
Bild
Stapeldiagram     
Du använder ofta stapeldiagram när du vill jämföra och få en överblick över resultatet av en undersökning.
​                                       Staplarna kan vara liggande eller                                            stående.
Picture
Stolpdiagram
Du använder stolpdiagram när du redovisar tal.
Picture
Linjediagram
När du vill beskriva en förändring över tid så är det bra att använda sig av linjediagram. Ett exempel på detta är temperaturstatistiken i tabellen ovan. Ett linjediagram består alltid av en linje i någon form.
​
Picture
Cirkeldiagram
Ett bra sätt att visa en överblick över en undersökning är att använda sig av ett cirkeldiagram. Ett cirkeldiagram visar delarna som tårtbitar där var och en kallas för en sektor.
Ord som förklarar förändring i diagram
Övningar
www.kimsmatematik.com